Dom Blog~~Detaljan vodič za puni dodatak~~

~~na 2024/05/10~~ ~~601~~

Detaljan vodič za puni dodatak

U području digitalne elektronike i računalnog inženjerstva, dodaci predstavljaju jedan od najvažnijih građevnih blokova, ključni u konstrukciji i funkcionalnosti zamršenijih aritmetičkih krugova.Kao integralne komponente aritmetičke logičke jedinice (ALU), dodaci olakšavaju brojne računalne operacije, u rasponu od osnovnih aritmetičkih do složenih logičkih zadataka potrebnih za operacije sustava.Njihov dizajn, koji može varirati od jednostavnih dodataka do složenijih punih dodataka, igra ključnu ulogu u poboljšanju učinkovitosti i brzine obrade unutar digitalnih sustava.Ovaj se članak upušta u detaljnu arhitekturu i funkcionalne nijanse različitih vrsta dodataka, ilustrirajući njihovu kritičnu ulogu u modernoj računalnoj tehnologiji i istražujući njihovu operativnu logiku, krugove i aplikacije u širem kontekstu dizajna digitalne logike.

Katalog

1. Što je dodatak?

2. Pola dodavanja

3. Potpuni dodatak

4. Tablica istine pune addera

5. Karakteristike jednadžbe punog dodavanja

6. Provedba potpunog kruga dodavanja

7. Prednosti i nedostaci punih dodataka

8. Primjene punih dodataka u digitalnoj logici

9. Primjeri implementacije punih dodataka

10. Zaključak

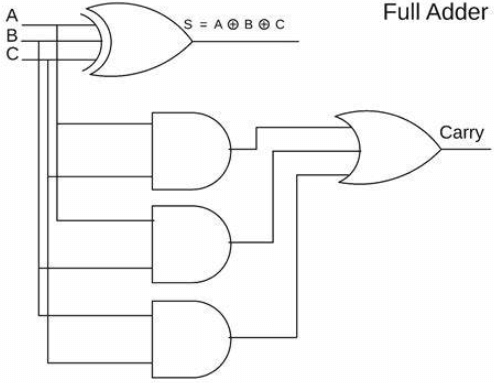
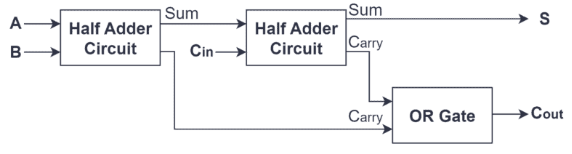
Slika 1: Potpuni dodatak

Što je dodatak?

Adder je temeljna komponenta u elektroničkom inženjerstvu i dizajnu digitalne logike i igra središnju ulogu u složenijim računalnim sustavima.Kao dio aritmetičke logičke jedinice (ALU), dodatak rješava razne osnovne računalne zadatke.Na učinkovitost i performanse cijelog procesora izravno utječu na dizajn i funkcionalnost dodavanja.

U procesoru se dodatak koristi ne samo za osnovne aritmetičke operacije poput dodavanja i oduzimanja, već se upušta u širi raspon logičkih operacija.Na primjer, prilikom pokretanja programa procesor često mora izračunati nove memorijske adrese.To se obično radi dodavanjem ili oduzimanjem trenutne adrese - zadatka koji je izvršio dodatak.Oni kontroliraju broj iteracija petlje i ukupni protok povećanjem i smanjenjem brojača.U složenijim aplikacijama, poput indeksiranja tablice, dodaci brzo pronalaze podatke izračunavanjem odstupanja.Ovo je važno za sustave upravljanja bazama podataka, konstrukciju prevoditelja i obradu podataka velikih razmjera.Dodaci su također ključni u implementaciji određenih tehnika mapiranja u sustavima predmemorije na više razina, koristeći aritmetičke operacije za određivanje položaja podataka u predmemoriji, optimizirajući na taj način učinkovitost pristupa.

Tehnološki se dodaci implementiraju kroz različite dizajne kruga, uključujući paralelne, serijske i cjevovodne dodatke.Paralelni dodaci favorizirani su za njihovu sposobnost istovremeno rukovanja s više znamenki, što ih čini prikladnim za scenarije koji zahtijevaju brzo računanje.Serijski dodaci, s druge strane, obrađuju jedan bit po ciklusu takta i idealni su za okruženje s ograničenim resursima ili niske snage.Dolaznici cjevovoda dijele postupak dodavanja u nekoliko faza, a svaki postupa s dijelom operacije dodavanja.Ovaj dizajn značajno povećava brzinu računanja, posebno u računalnim okruženjima visokih performansi.

Pola divila

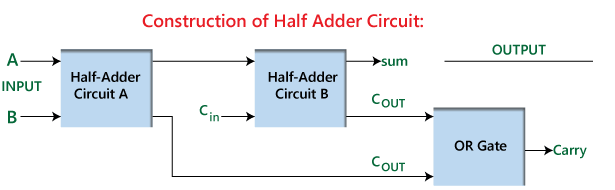
Polakopojasni krug temeljni je građevni blok u digitalnoj elektronici, posebno dizajniran za dodavanje dvije jedne binarne znamenke.Ovaj krug tvori temelj punog dodavanja i ključan je za razumijevanje složenijih dizajna logičkih krugova.U pola dodavanja postoje dva primarna ulaza, označena A i B, koji predstavljaju AUGEND, odnosno dodatak.Ova postavka omogućuje mu izračunavanje zbroja i izvođenje izlaza bez potrebe za unosom nošenja iz prethodnih izračuna.

Jezgra pola dodavanja sastoji se od dvije logičke kapije: XOR vrata i vrata.XOR vrata odgovorna su za generiranje izlaza SUM.Djeluje prema jednostavnom pravilu gdje izlazi 1 ako je samo jedan od njegovih ulaza 1;Inače, izlazi 0. Vrata i vrata, s druge strane, obrađuje izlaz.Izrađuje 1 samo kad su oba njegova ulaza 1, savršeno se usklađujući s temeljnim zahtjevima binarnog dodavanja.

Slika 2: Izgradnja pola dodavanja

Ovaj učinkovit i izravan dizajn omogućava da pola dodava ne samo da samostalno izvodi osnovni binarni dodatak, već i da posluži kao građevni blok za stvaranje punog dodavanja.Potpuni dodatak konstruira se kombiniranjem dva poluvremena s dodatnim ili vratima.U ovom postavku, prvu polovicu dodava početni zadatak dodavanja, generirajući preliminarni iznos i nošenje.Drugo poluvrijeme zatim obrađuje nošenje iz prvog, zajedno s dodatnim unosom nošenja.Konačno, ili vrata spajaju dva izvođenja izlaza kako bi proizveli konačni izlaz.Ovaj aranžman poboljšava funkcionalnost dodavanja, omogućujući mu da podnese složenije multi-bitne zadatke dodavanja, pokazujući široku primjenu i važnost pola dodavača u dizajnu digitalnog kruga.

Puni dodatak

Potpuni adder je napredna komponenta u dizajnu digitalne logike, opremljena za rukovanje dodavanjem tri jedno-bitna binarna ulaza, obično označenih kao A, B i nošenje (CIN).Ovaj dizajn omogućava potpunom dodavanju da učinkovito obrađuje složene binarne dodatke uključivanjem nošenja iz prethodnih izračuna nižeg reda u jednu operaciju.

Slika 3: Potpuni krug za dodavanje

Funkcionalno, puni dodatak može iznijeti dvoznamenkasti zbroj, što znači da se njegov izlaz može kretati od 0 do 3, a može proizvesti i izvođenje (Cout).To se događa jer, kada su svi ulazni bitovi postavljeni na 1 (a = 1, b = 1, cin = 1), zbrojni izlaz bit će 1 (predstavlja binarni 01), a generira se i izvršenje 1, što ukazuje na toDodatno nošenje potrebno je prenijeti na sljedeći viši zalogaj.

Strukturno, puni dodatak uglavnom se sastoji od dva poluvremena i jednog ili vrata.Prilog prvog poluvremena uzima ulaze A i B, generirajući početni zbroj i signal nosača.Ta se početna svota zatim unosi, zajedno s prijenosom (CIN), u drugom poluvremenu.Uloga drugog poluvremena je dodati ovu zbroj iz prvog poluvremena u CIN, proizvodeći još jednu zbroj i novi izlaz.Istodobno, izlaz iz prvog poluvremena i izlaz iz drugog poluvremena spojeni su kroz vrata ili vrata, a kulminirao je u konačnom izvođenju (COUT) punog dodavanja.Dizajn ove strukture osigurava da potpuni dodatak učinkovito postupa s širenjem nosača uz dodatak operacijama, što ga čini idealnim za izvršavanje multi-bitnih binarnih dodataka.Dakle, dizajn punog dodavanja ne samo da ubrzava obradu podataka i povećava učinkovitost, već i pojednostavljuje složenost implementacije hardvera kroz izravnu kombinaciju logičkih vrata, što ga čini neophodnom komponentom u višeznamenkastom dodatku i aritmetičkoj logičkoj jedinici (ALU).

Parametri	Pola divila	Puni dodatak
Opis	Pola adder je kombinirana logika krug koji dodaje dvije 1-bitne znamenke.Pola dodatka stvara zbroj njih dvojice ulazi.	Potpuni dodatak je kombinirana logika krug koji izvodi dodavanje operacije na tri jedno-bitna binarna broja. Potpuni dodatak daje zbroj od tri ulaza i nosi vrijednost.
Prethodni nošenje	Prethodno nošenje se ne koristi.	Koristi se prethodno nošenje.
Unosi	U pola dodavanja postoje dva ulaznog bita (a, B).	U punom adderu postoje tri ulazna bita (A, b, c_u).
Izlazi	Generirani izlaz je od dva bita-zbroja i nositi s ulaza od 2 bita.	Generirani izlaz je od dva bita-zbroja i nositi s unosa 3 bita.
Koristi se kao	Krug za pola dodavanja ne može se koristiti u na isti način kao krug punog dodavanja.	Potpuni krug za dodavanje može se koristiti na mjestu pola kruga za dodavanje.
Značajka	Jednostavan je i jednostavan za implementaciju	Dizajn punog dodavanja nije kao Jednostavno kao pola dodavanja.
Logičan izraz	Logički izraz za pola dodavanja je: S = a⊕b;C = a*b.	Logički izraz za puni dodatak je: S = a⊕b⊕cin;C_van= (ab)+(c_u(a⊕b)).
Logička vrata	Sastoji se od jednog bivšeg ili vrata i jednog i kapija	Sastoji se od dva bivša ili dva i vrata, i jedno ili vrata.
Prijava	Koristi se u kalkulatorima, računalima, Digitalni mjerni uređaji itd.	Koristi se u više bita, Digitalni procesori itd.
Alternativno ime	Za pola nema alternativnog imena guja.	Potpuni dodatak poznat je i kao pukotina guja.

Grafikon 1: Razlika između pola dodavanja i punog dodavanja

Puna tablica istine addera

Tablica istine punog dodavanja ključ je za razumijevanje njegove operativne logike, detaljno opisujući precizan odnos između binarnih ulaznih kombinacija i njihovih odgovarajućih izlaza.Ova tablica pokazuje sve potencijalne scenarije unosa i njihove ishode, što ga čini bitnim alatom u dizajnu i provjeri digitalnih logičkih krugova.Potpuni dodatak obrađuje tri ulaza: A, B i A nošenje (CIN), od kojih svaki može biti 0 ili 1. To rezultira u osam mogućih kombinacija ulaza.

Za svaku od ovih kombinacija, izlazi iz punog dodavanja uključuju zbroj (zbroj) i izvođenje (Cout).Zbroj je dodatak Modulo-2 (XOR operacija) tri ulaza-A, B i CIN.Izvođenje se događa kada su najmanje dva ulaznog bita 1. To odražava mogućnost punog dodavanja za rukovanje prenošenjem u sekvencijalnim operacijama dodavanja, osiguravajući točnost u višim bitnim proračunima.

Da biste ilustrirali, razmotrite scenarij unosa gdje su svi ulazi 0 (a = 0, b = 0, c-in = 0).Izlazni zbroj bit će 0, a nošenje će također biti 0, što ukazuje na to da nema dodatne zbroja ili nošenja za upravljanje.Ako je samo jedan ulazni bit 1, kao što je a = 1, b = 0, c-in = 0, izlazni zbroj bit će 1 bez nošenja, pokazujući da nema potrebe za prenosom nošenja na viši zalogaj.Kad su dva ulaznog bita 1, poput a = 1, b = 1, c-in = 0, izlazni zbroj je 0 (budući da je 1+1 jednak 2 u binarnom, a modulo-2 rezultira u 0), ali nošenje-Out je 1, što ukazuje na nošenje koje je potrebno prenijeti na sljedeći viši zalogaj.Najsloženiji scenarij događa se kada su sva tri ulaznog bita 1 (a = 1, b = 1, c-in = 1);Izlazni zbroj je 1, a postoji i obavljanje 1, što sugerira da je upravljanje nošenjem također potrebno na još višim bitovima.

A	B	C_u	S	C_van
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Grafikon 2: Tablica s punom adderom

Karakteristike jednadžbe punog dodavanja

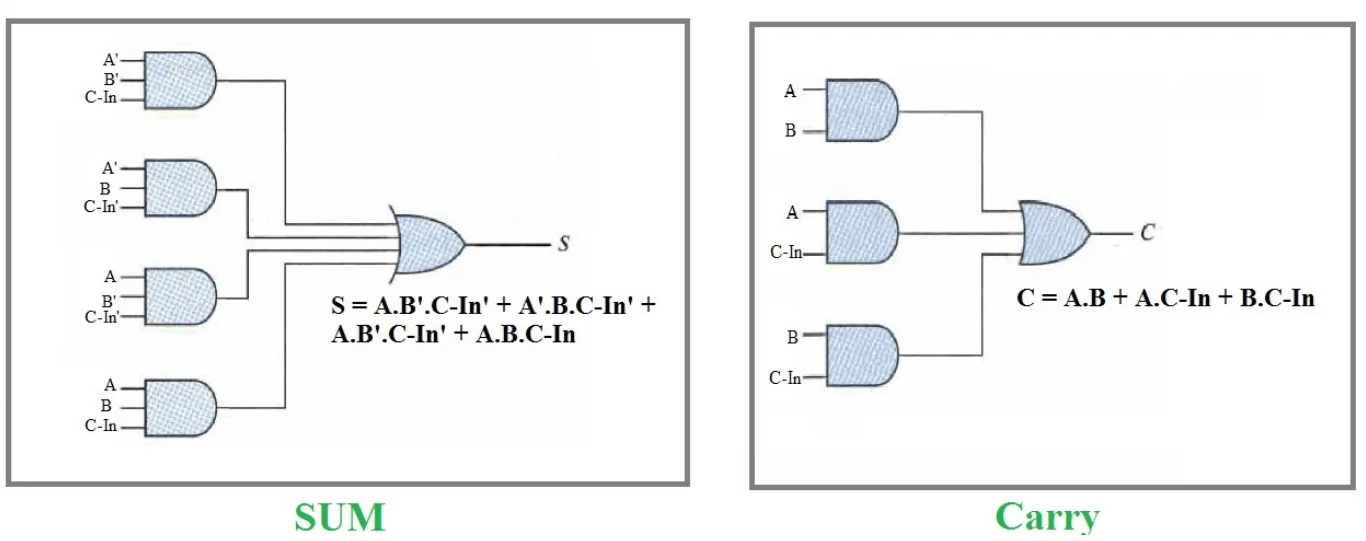
Razumijevanje punog dodavanja uključuje seciranje njegove funkcionalnosti pomoću tablice istine, gdje različite kombinacije ulaznih vrijednosti A, B i C-In dovode do izlaza zbroja i cout.Da bismo shvatili operaciju, pojednostavimo logičke jednadžbe korak po korak.

Logički izraz za iznos

Jednadžba započinje različitim slučajevima kada je zbroj jednak 1:

• A 'B' CIN + A 'B CIN' + A B 'CIN' + AB CIN

Ova se jednadžba može kondenzirati grupiranjem uvjetima sa i bez CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

Ovo pojednostavljenje dovodi do lakše implementacije:

• CIN XOR (XOR B)

Ovaj prikaz pokazuje da je zbrojni izlaz u osnovi XOR operacija među A, B i CIN, bilježeći jezgrena ponašanja binarnog dodatka gdje se zbroj prebacuje na temelju neparnog broja.

Logika za cout

Počevši s uvjetima u kojima se generira nošenje:

• A 'B CIN + A B' CIN + AB C-IN ' + AB CIN

Pojednostavljujući jednadžbu, identificiramo izraze koji obično uključuju stvaranje nošenja:

• AB + B CIN + A CIN

Tražeći drugu metodu za implementaciju cout-a, jednadžba se može reorganizirati:

• AB + A CIN + B C-IN (A + A ')

To se proširuje i rekombinira kako bi se snimile sve scenarije gdje su najmanje dva ulaza 1:

• ab cin + ab + a c-in + a 'b cin

• ab (1 + cin) + a c-in + a 'b cin

• ab + a c-in (b + b ') + a' b cin

• ab + a b 'cin + a' b cin

• AB + CIN (A 'B + A B')

Konačni kompaktni oblik za cout:

• AB + CIN (XOR B)

Ova verzija jednadžbe izvedbe pokazuje kako se proizvodi cout ili kada su i A i B 1, ili kada je jedan od A ili B-a 1 zajedno s prijenosom, inkapsulirajući tako logiku potrebnu za upravljanje širenjem u multi-Binarni dodatak.Ova pojednostavljena logika posebno je korisna za implementaciju učinkovitih digitalnih krugova.

Slika 4: Jednadžbe punog dodavanja

Implementacija punog kruga za dodavanje

Primjena potpunog kruga za dodavanje uključuje pažljivo sastavljanje dva poluvremena i vrata ili vrata za stvaranje uređaja koji može učinkovito rukovati dodavanjem tri jedno-bitna binarna ulaza.Ovaj aranžman optimizira složenost kruga i osigurava i učinkovite i točne izračunavanja.

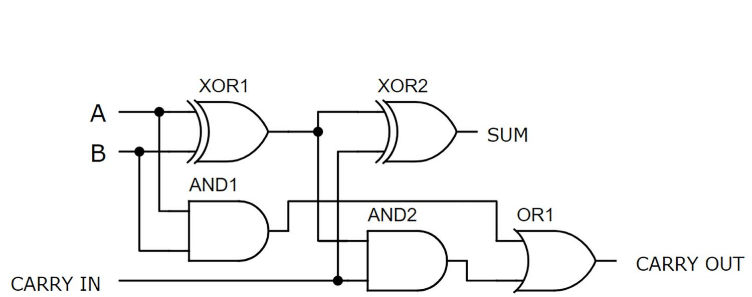
Za početak, prvo poluvrijeme uzima dva primarna binarna ulaza, A i B, koji su glavne znamenke koje se dodaju.Njegov je ključni zadatak izračunati zbroj i početno nošenje ta dva broja.Ovdje prvo poluvrijeme donosi dva ishoda: početni zbroj (Sum1) i početno nošenje (nošenje1).SUM1 se izvodi iz XOR operacije A i B, što ukazuje na to ima li ukupni broj neparnih broja 1.Carry1, rezultat rada i rada između A i B, ukazuje na to jesu li obje znamenke 1, što zahtijeva nošenje do sljedećeg većeg zalogaja.

Zatim se u drugom poluvremenu pridružuje postupak.Koristi zbroj izlaza SUM1 i treći ulaz CIN (prenošenje iz prethodnog izračuna) kao svoje ulaze.Drugo poluvrijeme daje dva izlaza: konačni zbrojni rezultat (Sum2) i sekundarni nošenje (nosač2).Sum2, što je XOR rezultat Sum1 i CIN, predstavlja konačnu zbroj tri ulaza, prikazujući agregirani binarni dodatak.Carry2, koji proizlazi iz rada između zbroja1 i CIN, ukazuje na nošenje koje generira ove komponente.

Full Adder Circuit with Using Two Half Adder

Slika 5: Potpuni krug za dodavanje s korištenjem dva pola dodavanja

Konačno, za dovršetak dizajna cijelog dodavanja, potrebna je vrata ili vrata za rukovanje izlazima s nosačem1 i nosačem2 iz oba pola dodavača.Ovo ili vrata osigurava da se bilo koji nošenje generirano tijekom izračuna ispravno proslijedi na konačni izlaz.Stoga je konačni izlaz punog dodavanja (COUT) ili rezultat nošenja1 i nosača2.Uključivanje ovog ili vrata jamči da se sav potencijalni nosači točno izračunavaju i prenose na sljedeću razinu u multi-bitnim dodavanju operacijama, osiguravajući integritet aritmetičke operacije u više bita.

Prednosti i izazovi punih dodataka u digitalnoj logici

Potpuni dodaci igraju neophodnu ulogu u dizajnu digitalne logike, nudeći brojne prednosti koje ih čine ključnim u različitim scenarijima računanja i obrade podataka.Njihove primarne prednosti uključuju izvanrednu fleksibilnost, brzu brzinu obrade i učinkovito upravljanje nošenjem.Ove osobine čine potpune dodatke idealnim za izvršavanje složenih aritmetičkih operacija i logičkih funkcija, posebno u aplikacijama koje zahtijevaju sekvencijalno multi-bitno dodavanje.

Prednosti

Fleksibilnost: Potpuni dodaci izvrsno su u svojoj sposobnosti da istovremeno obrađuju više binarnih ulaza (A, B i CIN).Oni se također mogu proširiti u veće nizove za dodavanje kako bi se obrađivale dulje binarne brojeve.Ova skalabilnost važna je za izgradnju aritmetičkih logičkih jedinica visokih performansi (ALUS), koje moraju provesti zamršene multi-bitne aritmetičke i logičke operacije.

Brzina: Zahvaljujući njihovoj unutarnjoj paralelnoj arhitekturi obrade, puni dodaci mogu dovršiti dodavanje svih ulaza u jednom ciklusu takta, a istovremeno odlučuju izvršiti izlaze.Ova sposobnost podržava kontinuirane operacije dodavanja i neophodna je za obradu podataka u stvarnom vremenu u modernim mikroprocesorima i računalnim uređajima velike brzine.

Nedostaci

Međutim, puni dodaci također predstavljaju značajne nedostatke:

Složenost u dizajnu i implementaciji: Potpuni dodaci uključuju više logičkih vrata i širenje na više razine, čineći svoj dizajnerski kompleks.Ova složenost ne samo da povećava troškove proizvodnje, već može utjecati i na pouzdanost krugova.

Problemi kašnjenja širenja: Proširenje može proći kroz nekoliko logičkih vrata, a svaka je dodala svoje kašnjenje.To može ograničiti ukupnu računalnu brzinu tijekom velikih operacija, posebno u opsežnim računalnim sustavima i u dizajnu vrlo velikog integracije (VLSI) i velikih brzina.Kašnjenje može postati značajno usko grlo u performansama.

Da bi ublažili ove probleme, inženjeri kontinuirano istražuju učinkovitije dizajne kruga.Strategije uključuju korištenje brže tehnologije logičkih vrata, optimizaciju izgleda kruga za skraćivanje duljine puta i razvijanje naprednih tehnologija poput dodataka za nošenje kako bi se umanjila kašnjenja u širenju nošenja.

Primjene punih dodataka u digitalnoj logici

Potpuni dodaci opsežno se koriste u digitalnoj logici, cijenjenim za njihovu fleksibilnost i učinkovitost, što ih čini središnjim u mnoštvu računalnih i zadataka obrade podataka.Njihova se primjena proteže od osnovnih aritmetičkih operacija do složene obrade signala i kontrole sustava.Evo detaljnog pogleda na neka ključna područja u kojima su puni dodaci sastavni dio.

Aritmetički krugovi

Jedna od najravnijih uporaba punih dodataka je u aritmetičkim krugovima gdje izvode binarni dodatak.Osobito ključno u dodatku više bitnog broja, puni dodaci upravljaju duljim binarnim sekvencama kroz kaskadno.U ovom rasporedu, svaki puni dodatak obrađuje dodatak za svoj bit i nošenje s donjeg dijela, a zatim prenosi novi nošenje na sljedeći viši zalogaj.Ova kaskada omogućuje sveobuhvatno više bitni dodatak u cijelom rasponu znamenki.

Obrada podataka

Potpuni dodaci također igraju glavnu ulogu u naprednim zadacima obrade podataka kao što su digitalna obrada signala (DSP) za filtriranje i Fourierove transformacije, gdje su potrebne precizne i brze aritmetičke operacije.Uz to, u području informacijske sigurnosti, uključujući algoritme šifriranja i ispravljanja pogrešaka i ispravljanja pogrešaka poput provjere pariteta i stvaranja koda za provjeru cikličke suvišnosti (CRC), puni dodaci su ključni za izvršavanje esencijalnih operacija BIT -a.

Brojači

U digitalnim brojačima, puni dodaci neophodni su za implementaciju funkcija priraštaja i smanjenja, posebno u modularnim i sinkronim brojačima.Oni precizno upravljaju nosačima i zaduživanjem kako bi osigurali precizno brojanje.

Multiplekseri (MUX) i demultiplekseri (Demux)

U multiplekserima i demultipleksima, puni dodaci igraju kritičnu ulogu u odabiru kanala i raspodjeli podataka.Sudjeluju u logici koja određuje koji se kanali koriste za unos i izlaz podataka, donoseći odluke na temelju signala logičke kontrole.

Memorijska tehnologija

U memorijskoj adresi, puni dodaci pomažu u generiranju adresnih signala za dinamički pristup memorijskim mjestima.To je posebno važno u dinamičkoj memoriji nasumično pristupa (DRAM) i drugim sustavima za pohranu, gdje puni dodaci podržavaju složene izračunavanja adresa kako bi se poboljšala učinkovitost pristupa memoriji.

Aritmetičke logičke jedinice (ALU)

Konačno, kao temeljne komponente aritmetičkih logičkih jedinica u mikroprocesorima i digitalnim procesorima signala, puni dodaci su presudni.ALU upravlja svim aritmetičkim i logičkim operacijama, a puni dodaci osiguravaju da se podaci obrađuju brzo i točno.

Primjeri pune implementacije dodavanja

Potpuni dodaci mogu se konstruirati pomoću različitih logičkih vrata i konfiguracija.Ovdje istražujemo četiri različite implementacije, ističući njihove postavke i operativne nijanse.

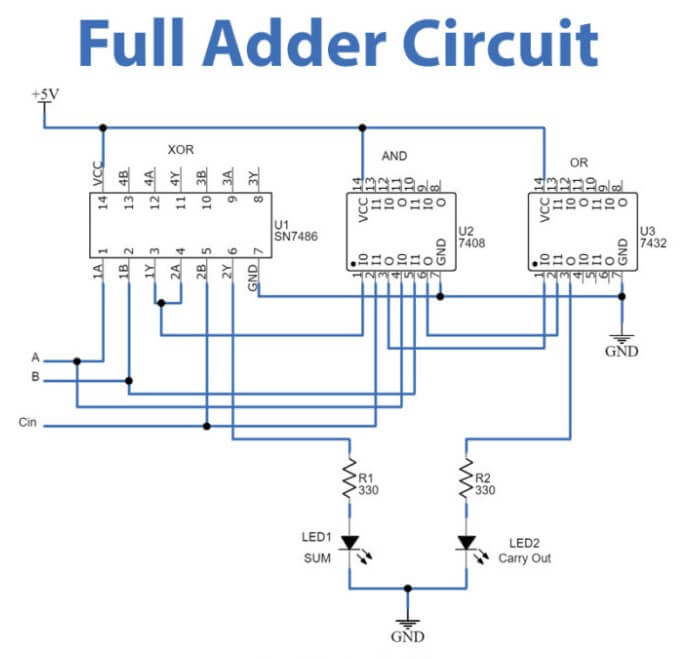
Puni adder izgrađen s XOR -om i ili ili vrata

Full Adder Built with XOR, AND, and OR Logic Gates

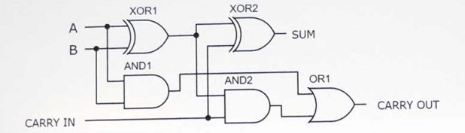
Slika 6: Potpuni dodatak izgrađen s XOR -om, i ili ili logičkim vratima

Ovaj primjer prikazuje puni dodatak izgrađen na ploči s diskretnim tranzistorima.Konfiguracija sadrži pet logičkih vrata: dvije XOR kapije, dva i vrata, i jedna ili vrata, koja zahtijevaju ukupno 21 tranzistor.Ulazi A i B spojeni su na gornju lijevu stranu ploče, primajući A +5V opskrbu.Ovi se ulazi upravljaju pomoću dva prekidača.Dvije LED diode u gornjem lijevom redu označavaju stanja ulaza A i B, dok dvije LED diode na desnoj strani prikazuju izlaze.Otpornici koji se koriste u krugu su svi 2,2K Ohma.Kad su ulazi A i B uključeni i prijevoz je isključen, izlaz pokazuje binarnu vrijednost od 10, što predstavlja zbroj 2 (1 + 1 + 0 = 10).Vrata XOR-a, sagrađena s prvih 12 tranzistora, upravljaju primarnim zbrajanjem, dok donja polovica ploče sadrži i ili ili vrata za operacije nošenja, ožičenje u boji u boji povećava jasnoću i rješavanje problema.

Potpuni adder pomoću Nand Gatesa

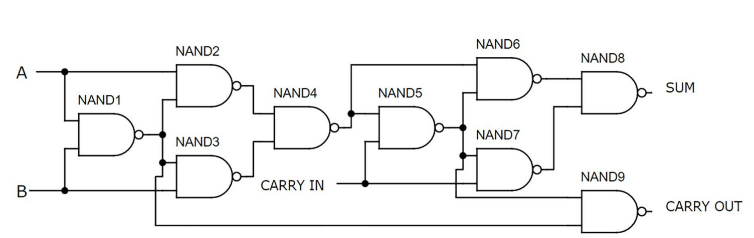
Slika 7: Potpuni dodatak pomoću Nand Gatesa

Ovaj puni dodatak koristi devet NAND vrata, pri čemu je svaka vrata napravljena od dva tranzistora, ukupno 18 tranzistora.Ova metoda je među najjednostavnijim i najučinkovitijim načinima konstrukcije punog dodavanja koristeći diskretne komponente.Sva se vrata sastavljaju na gornjoj polovici ploče, dok prekidači zauzimaju donju polovicu.Funkcionalnost kruga prikazana je s ulazima A i B uključeno i isključenje, što rezultira izlaznom binarnom vrijednošću od 10, što je ekvivalentno decimalnoj 2.

Potpuni dodatak s niti vrata

Slika 8: Potpuni dodatak s niti vrata

Izgrađeno s devet ili vrata, od kojih je svaka potrebna dva tranzistora, a ovo postavljanje također koristi 18 tranzistora.Izgradnja punog dodavanja s Nor Gatesom nudi dobru alternativu, ali uključuje složenije ožičenje u usporedbi s Nand Gatesom.Svaki tranzistor u NOR kapiji je uzemljen, a kolekcionari su povezani narančastim žicama kako bi osigurali uredno i organizirano ožičenje.Ova je konfiguracija prikazana s ulazima A i B aktiviranim i nošenim deaktiviranim, što dovodi do izlaza u kojima je nošenje aktivno, a zbroj isključen.

Zaključak

Kroz ovo istraživanje Adder tehnologije, od osnovnih polovica do sofisticiranih dizajna punih dodataka, očito je da su te komponente temeljne do napretka digitalne elektronike.Operativne karakteristike i primjeri provedbe dali su svestranost i učinkovitost dodataka u različitim računalnim postavkama.Ispitujući strukturu i funkciju dodataka, posebno kroz njihove tablice istine i karakteristične jednadžbe, dobivamo vrijedne uvide u njihove mogućnosti i ograničenja.Ovo znanje je od presudne važnosti u napredovanju dizajna učinkovitijih i bržih računalnih sustava.U konačnici, dodaci ne samo da pojednostavljuju složene binarne proračune, već i omogućuju širenje tehnologije u područjima koja su raznolika kao što je obrada podataka, raspodjela memorije i digitalna obrada signala.Kako se digitalna tehnologija razvija, u tijeku je usavršavanje i inovacije u dizajnu Adder i dalje kamen temeljac u razvoju naprednijih računalnih arhitektura, osiguravajući da ove temeljne komponente ostanu u središtu dizajna i implementacije digitalnog sustava.

Često postavljana pitanja [FAQ]

1. Što je puni krug za dodavanje?

Potpuni dodatak je digitalni krug koji dodaje tri binarna bita za proizvodnju zbroja i izlaza.Dizajniran je za obradu dodavanja tri ulaza: dva značajna bita i jedan prijevoz iz prethodnog dodatka.To omogućava da se koristi u uzastopnim fazama za dodavanje multi-bitnih binarnih brojeva.

2. Koliko i, ili, XOR u punom dodavanju?

Tipičan puni dodatak sadrži:

Dva XOR vrata za generiranje zbroja.

Dva i vrata kako bi doprinijeli izračunavanju iznosa.

Jedno ili vrata za finaliziranje izlaza.

3. Što je ulaz u punom adderu?

Ulaz nosača (CIN) u punom dodavanju je bit nosača od dodavanja prethodnih nižih značajnih bita u multi-bitnom binarnom dodatku.Omogućuje punom dodatnom priredu da razmotri ovo prethodno nošenje prilikom izračunavanja trenutne iznose i novog izvođenja.

4. Zašto koristiti puni dodatak umjesto pola dodavanja?

Koristi se puni dodatak umjesto pola dodavanja jer može dodati tri bita (uključujući nošenje iz prethodnih dodataka), što ga čini prikladnim za vezanje zajedno za dodavanje multi-bitnih brojeva.Pola dodatka može dodati samo dva bita i nema odredbu za prijenos, što ograničava njegovu upotrebu u najjednostavnije oblike binarnog dodavanja bez uzastopnog širenja nošenja.

O nama

ALLELCO LIMITED

Allelco je međunarodno poznat na jednom mjestu Distributer hibridnih elektroničkih komponenti za nabavu, opredijeljen za pružanje sveobuhvatnih usluga nabave i lanca opskrbe za globalnu elektroničku industriju proizvodnje i distribucije, uključujući globalne TOP 500 OEM tvornice i neovisne posrednike.
Čitaj više